Panel Regression: Traffic Deaths & Wages

Author

Zahid Asghar

School of Economics, QAU, Islamabad

Code 
library(leaflet)
leaflet() %>%
  addTiles() %>%
  addMarkers(lng = 73.136946, lat =33.748294 ,
             popup = "School of Economics, QAU, Islamabad")

Panel Data Regression

A panel dataset contains observations on multiple entities (individuals), where each entity is observed at two or more points in time.

Hypothetical examples:

  • Data on 50 districts in 2010 floods and again in 2022, for 100 observations total.

  • Data on 100 SMES, each SME is observed in 3 years, for a total of 150 observations.

  • Data on 1000 individuals, in four different months, for 4000 observations total.

Notations for Panel Data

A double subscript distinguishes entities (states) and time periods (years)

\(i\) = entity (state), \(n\) = number of entities, so \(i = 1,\dots,n\)

\(t\) = time period (year), \(T\) = number of time periods so \(t =1,\dots,T\)

Data: Suppose we have 1 regressor. The data are:

\((X_{it}, Y_{i}t), i = 1,\dots,n,\ t = 1,…,T\)

Panel data with \(K\) regressors \((X_{1it},X_{2it},\dots,X_{kit} Y_{i}t), i = 1,\dots,n,\ t = 1,…,T\) \(n\) = number of entities (states) \(T\) = number of time periods (years) Also called longitudinal data

Why are panel data useful?

With panel data we can control for factors that: - Vary across entities (states) but do not vary over time - Could cause omitted variable bias if they are omitted - are unobserved or unmeasured – and therefore cannot be included in the regression using multiple regression

Here’s the key idea: > If an omitted variable does not change over time, then any changes in Y over time cannot be caused by the omitted variable.

Example of a panel data set

Observational unit: a year in a U.S. state - 48 U.S. states, so \(n\) = # of entities = 48$ - 7 years (1982,…, 1988), so \(T\) = # of time periods = 7 - Balanced panel, so total # observations = \(7\times48\) = 336 Variables: - Traffic fatality rate (# traffic deaths in that state in that year, per 10,000 state residents) - Tax on a case of beer - Other (legal driving age, drunk driving laws, etc.)

An overview of data

Rows: 336
Columns: 34
$ state        <fct> al, al, al, al, al, al, al, az, az, az, az, az, az, az, a…
$ year         <fct> 1982, 1983, 1984, 1985, 1986, 1987, 1988, 1982, 1983, 198…
$ spirits      <dbl> 1.37, 1.36, 1.32, 1.28, 1.23, 1.18, 1.17, 1.97, 1.90, 2.1…
$ unemp        <dbl> 14.4, 13.7, 11.1, 8.9, 9.8, 7.8, 7.2, 9.9, 9.1, 5.0, 6.5,…
$ income       <dbl> 10544.15, 10732.80, 11108.79, 11332.63, 11661.51, 11944.0…
$ emppop       <dbl> 50.69204, 52.14703, 54.16809, 55.27114, 56.51450, 57.5098…
$ beertax      <dbl> 1.53937948, 1.78899074, 1.71428561, 1.65254235, 1.6099070…
$ baptist      <dbl> 30.3557, 30.3336, 30.3115, 30.2895, 30.2674, 30.2453, 30.…
$ mormon       <dbl> 0.32829, 0.34341, 0.35924, 0.37579, 0.39311, 0.41123, 0.4…
$ drinkage     <dbl> 19.00, 19.00, 19.00, 19.67, 21.00, 21.00, 21.00, 19.00, 1…
$ dry          <dbl> 25.0063, 22.9942, 24.0426, 23.6339, 23.4647, 23.7924, 23.…
$ youngdrivers <dbl> 0.211572, 0.210768, 0.211484, 0.211140, 0.213400, 0.21552…
$ miles        <dbl> 7233.887, 7836.348, 8262.990, 8726.917, 8952.854, 9166.30…
$ breath       <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…
$ jail         <fct> no, no, no, no, no, no, no, yes, yes, yes, yes, yes, yes,…
$ service      <fct> no, no, no, no, no, no, no, yes, yes, yes, yes, yes, yes,…
$ fatal        <int> 839, 930, 932, 882, 1081, 1110, 1023, 724, 675, 869, 893,…
$ nfatal       <int> 146, 154, 165, 146, 172, 181, 139, 131, 112, 149, 150, 17…
$ sfatal       <int> 99, 98, 94, 98, 119, 114, 89, 76, 60, 81, 75, 85, 87, 67,…
$ fatal1517    <int> 53, 71, 49, 66, 82, 94, 66, 40, 40, 51, 48, 72, 50, 54, 3…
$ nfatal1517   <int> 9, 8, 7, 9, 10, 11, 8, 7, 7, 8, 11, 19, 16, 14, 5, 2, 2, …
$ fatal1820    <int> 99, 108, 103, 100, 120, 127, 105, 81, 83, 118, 100, 104, …
$ nfatal1820   <int> 34, 26, 25, 23, 23, 31, 24, 16, 19, 34, 26, 30, 25, 14, 2…
$ fatal2124    <int> 120, 124, 118, 114, 119, 138, 123, 96, 80, 123, 121, 130,…
$ nfatal2124   <int> 32, 35, 34, 45, 29, 30, 25, 36, 17, 33, 30, 25, 34, 31, 1…
$ afatal       <dbl> 309.438, 341.834, 304.872, 276.742, 360.716, 368.421, 298…
$ pop          <dbl> 3942002, 3960008, 3988992, 4021008, 4049994, 4082999, 410…
$ pop1517      <dbl> 208999.6, 202000.1, 197000.0, 194999.7, 203999.9, 204999.…
$ pop1820      <dbl> 221553.4, 219125.5, 216724.1, 214349.0, 212000.0, 208998.…
$ pop2124      <dbl> 290000.1, 290000.2, 288000.2, 284000.3, 263000.3, 258999.…
$ milestot     <dbl> 28516, 31032, 32961, 35091, 36259, 37426, 39684, 19729, 1…
$ unempus      <dbl> 9.7, 9.6, 7.5, 7.2, 7.0, 6.2, 5.5, 9.7, 9.6, 7.5, 7.2, 7.…
$ emppopus     <dbl> 57.8, 57.9, 59.5, 60.1, 60.7, 61.5, 62.3, 57.8, 57.9, 59.…
$ gsp          <dbl> -0.022124760, 0.046558253, 0.062797837, 0.027489973, 0.03…

A large number of variables and 336 total observations. We need to select only a few variables required in doing this exercise.

Code 
## Summarise the variable state and year
fatalities %>% select(state,year) %>% 
  group_by(year) %>% 
  summarise(count=n())
# A tibble: 7 × 2
  year  count
  <fct> <int>
1 1982     48
2 1983     48
3 1984     48
4 1985     48
5 1986     48
6 1987     48
7 1988     48
Code 
## Traffic Deaths and Alcohal Taxes
# define the fatality rate
df <-fatalities %>% mutate(fatal_rate=fatal/pop*10000)

# subset the data

Fatalities1982 <- df %>% filter(year=="1982")

Fatalities1988 <- df %>% filter(year=="1988")

U.S traffic death data for 1982

Code 
ggplot(Fatalities1982)+aes(x= beertax,y=fatal_rate)+geom_point()+geom_smooth(method = "lm", se=FALSE)+labs(x="Beer Tax \n(Dollars per case 1988)",y="Fatality Rate \n Fatalities per 10000", title="US traffice death for 1982")
`geom_smooth()` using formula 'y ~ x'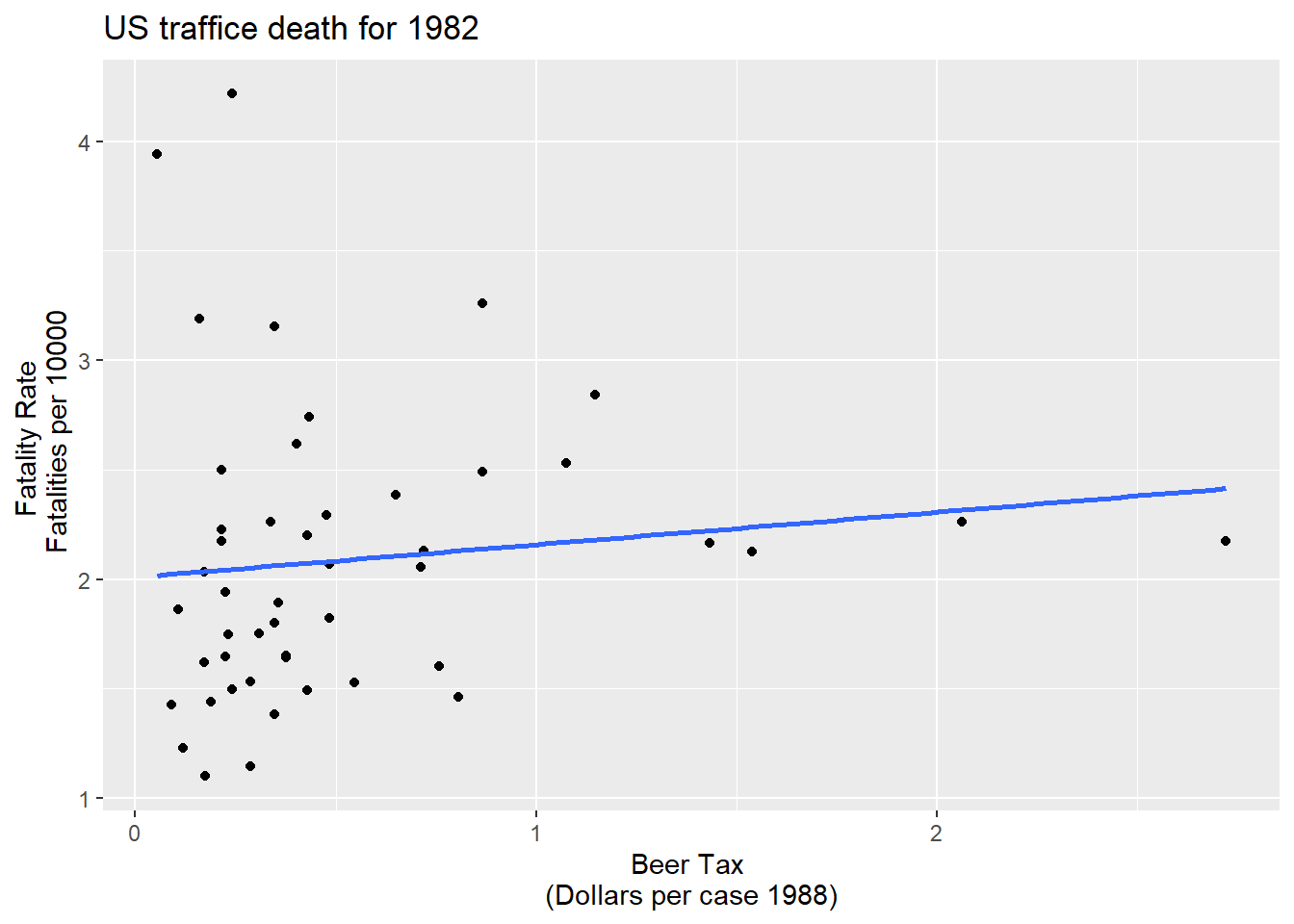

U.S traffic death data for 1988

Code 
ggplot(Fatalities1988)+aes(x= beertax,y=fatal_rate)+geom_point()+geom_smooth(method = "lm", se=FALSE)+labs(x="Beer Tax \n(Dollars per case 1988)",y="Fatality Rate \n Fatalities per 10000", title="US traffice death for 1988")
`geom_smooth()` using formula 'y ~ x'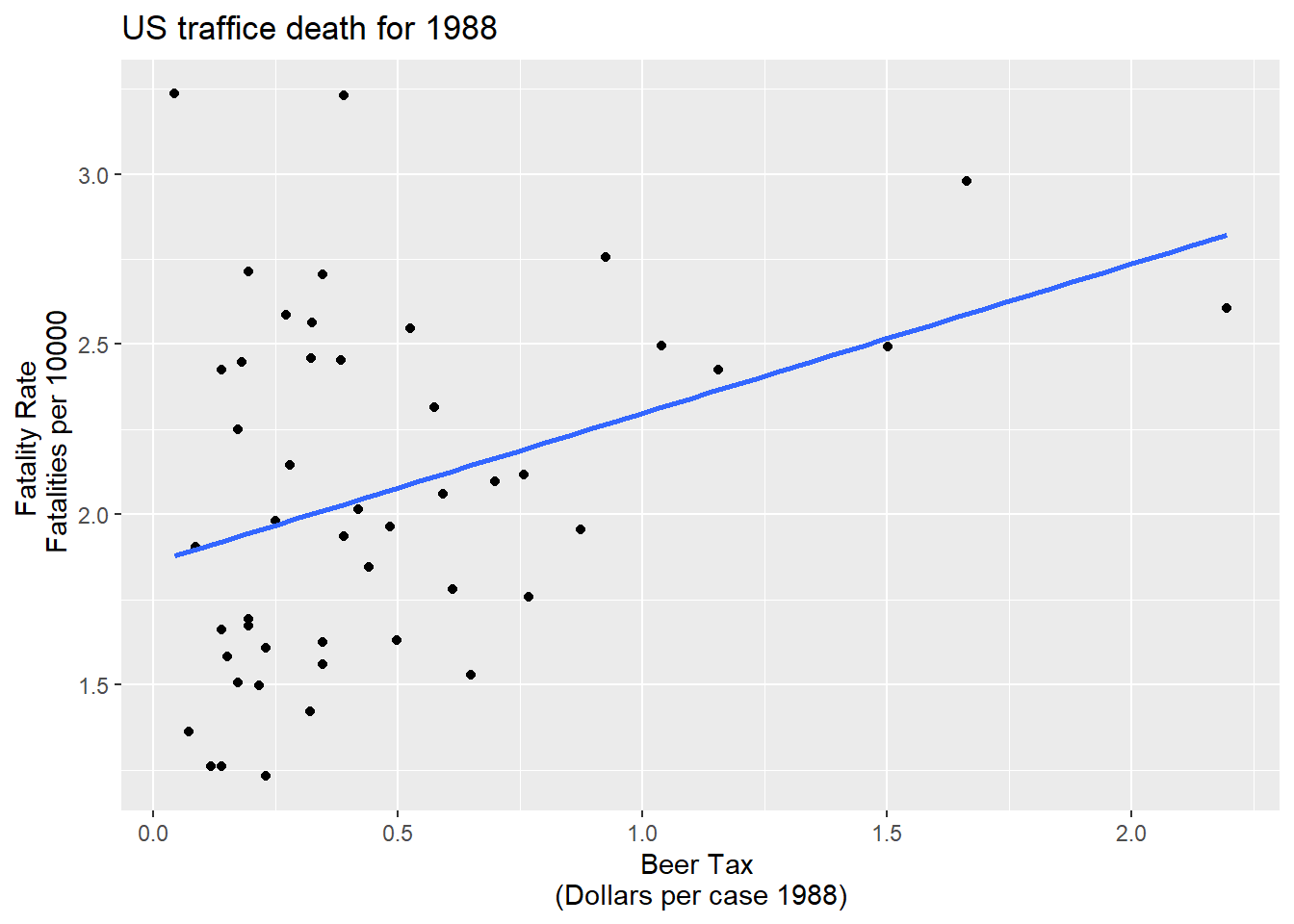

Regression line

Code 
# estimate simple regression models using 1982 and 1988 data
fatal1982_mod <- lm(fatal_rate ~ beertax, data = Fatalities1982)
fatal1988_mod <- lm(fatal_rate ~ beertax, data = Fatalities1988)

\(\widehat{FatalityRate}= 2.01 + 0.15beertax\)

\(\widehat{FatalityRate}= 1.86 + 0.43beertax\)

High alcohal tax, more deaths :smiley:

Why might there be higher more traffic deaths in states that have higher alcohol taxes?

Other factors that determine traffic fatality rate: - Quality (age) of automobiles - Quality of roads - “Culture” around drinking and driving - Density of cars on the road

These omitted variables could cause omitted variable bias

Example #1: traffic density. Suppose:

  1. High traffic density means more traffic deaths

  2. (Western) states with lower traffic density have lower alcohol taxes

Then the two conditions for omitted variable bias are satisfied.

  • Specifically, “high taxes” could reflect “high traffic density” (so the OLS coefficient would be biased positively – high taxes, more deaths)
  • Panel data lets us eliminate omitted variable bias when the omitted variables are constant over time within a given state.

Cultural attitude towards driving and drinking

  1. arguably are a determinant of traffic deaths; and
  2. potentially are correlated with the beer tax, so beer taxes could be picking up cultural differences (omitted variable bias).
  • Then the two conditions for omitted variable bias are satisfied. Specifically, “high taxes” could reflect “cultural attitudes towards drinking” (so the OLS coefficient would be biased)
  • Panel data lets us eliminate omitted variable bias when the omitted variables are constant over time within a given state.

Panel Data with Two Time Periods

Consider the panel data model: \(\widehat{FatalityRate_{it}} = \beta_0 + \beta_1 BeerTax_{it} + \beta_2Zi + u_{it}\)

\(Z_i\) is a factor that does not change over time (density), at least during the years on which we have data. • Suppose \(Z_i\) is not observed, so its omission could result in omitted variable bias. • The effect of \(Z_i\) can be eliminated using \(T = 2\) years.

The key idea:
Any change in the fatality rate from 1982 to 1988 cannot be caused by \(Z_i\), because \(Z_i\) (by assumption) does not change between 1982 and 1988.

The math: consider fatality rates in 1988 and 1982: \(FatalityRate_{i1988} = \beta_0 + \beta_1 BeerTax_{it} + \beta_2Zi + u_{i1988}\) \(FatalityRate_{i1982} = \beta_0 + \beta_1 BeerTax_{it} + \beta_2Zi + u_{i1982}\)

Suppose \(E{(u_{it}}{/BeerTax_{it},Z_i})=0\) E(uit|BeerTaxit, Zi) = 0.

Subtracting 1988 – 1982 (that is, calculating the change), eliminates the effect of \(Z_i\dots\)

\(FatalityRate_{i1988} = \beta_0 + \beta_1 BeerTax_{it} + \beta_2Zi + u_{i1988}\) \(FatalityRate_{i1982} = \beta_0 + \beta_1 BeerTax_{it} + \beta_2Zi + u_{i1982}\)

so \(FatalityRate_{i1988} – FatalityRate_{i1982}=\\\beta_1(BeerTaxi1988 – BeerTaxi1982) + (u_{i1988} – u_{i1982})\)

• The new error term, \((u_{i1988} – u_{i1982})\), is uncorrelated with either \(FatalityRate_{i1988}\) or \(FatalityRate_{i1982}\) • This “difference” equation can be estimated by OLS, even though \(Z_i\) isn’t observed. • The omitted variable \(Z_i\) doesn’t change, so it cannot be a determinant of the change in \(Y\)

1982 data

\(\widehat{FatalityRate}= 2.01 + 0.15beertax \ n=48\)

1988 data

\(\widehat{FatalityRate}= 1.86 + 0.43beertax \ n=48\)

Difference regression

\(\widehat{FatalityRate_{i1988} - FatalityRate_{i1982}} =\\ -\underset{(0.065)}{0.072} -\underset{(0.36)}{1.04} \times (BeerTax_{i1988}-BeerTax_{i1982}).\)

Code 
##Panel Data for two years
# compute the differences 
diff_fatal_rate <- Fatalities1988$fatal_rate - Fatalities1982$fatal_rate
diff_beertax <- Fatalities1988$beertax - Fatalities1982$beertax

# estimate a regression using differenced data
fatal_diff_mod <- lm(diff_fatal_rate ~ diff_beertax)

coeftest(fatal_diff_mod, vcov = vcovHC, type = "HC1")

t test of coefficients:

              Estimate Std. Error t value Pr(>|t|)   
(Intercept)  -0.072037   0.065355 -1.1022 0.276091   
diff_beertax -1.040973   0.355006 -2.9323 0.005229 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Code 
df2<-cbind(diff_fatal_rate,diff_beertax)

df2<-as.data.frame(df2)
## Plot
p2<-ggplot(df2)+aes(x=diff_fatal_rate,y=diff_beertax)+geom_point()+
  geom_smooth(method = "lm",se=FALSE)
p2+labs(x = "Change in beer tax (in 1988 dollars)",
        y = "Change in fatality rate (fatalities per 10000)")+ggtitle("Changes in Traffic Fatality Rates and Beer Taxes in 1982-1988")
`geom_smooth()` using formula 'y ~ x'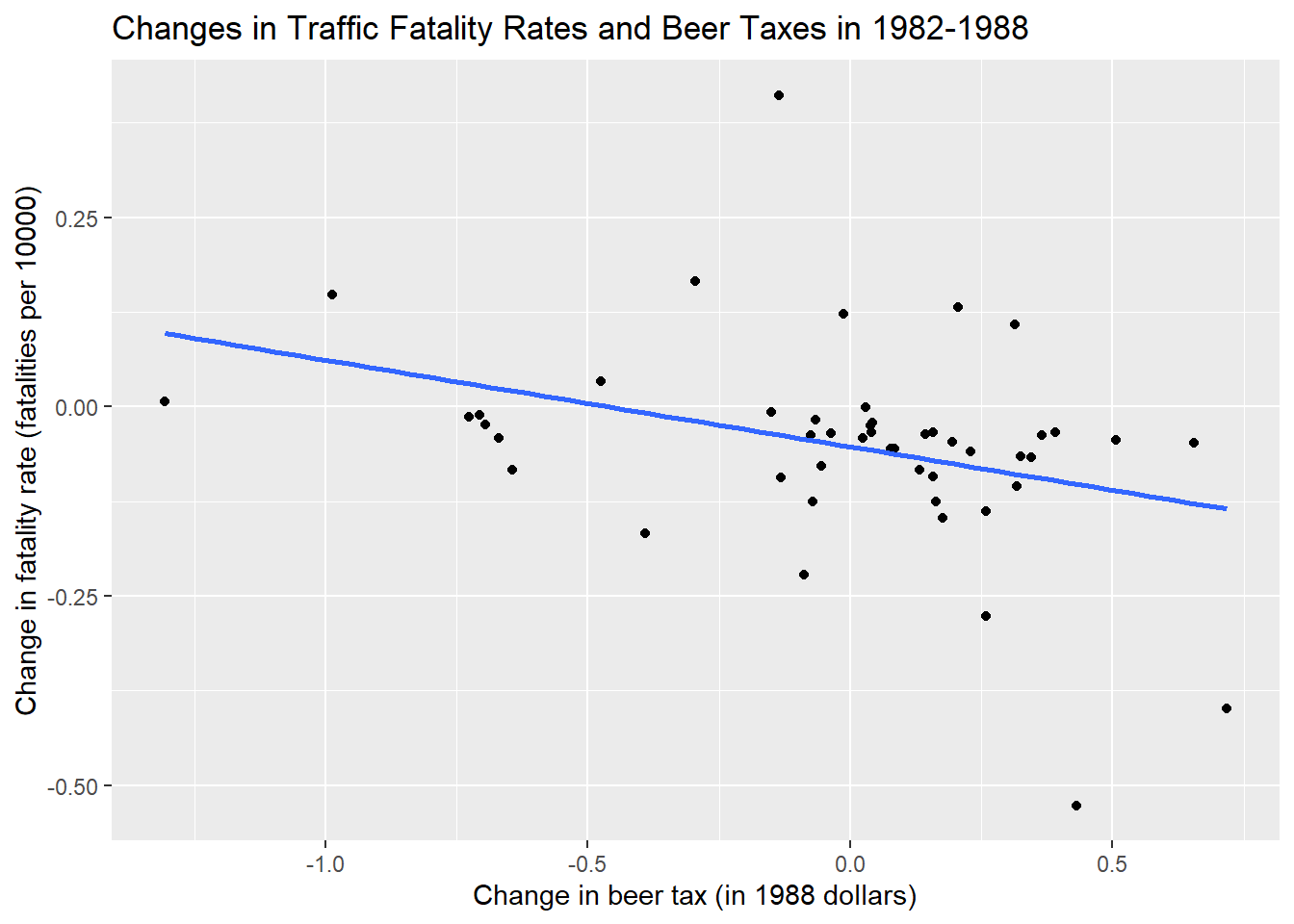

Fixed Effects Regression

What if you have more than 2 time periods \((T > 2)?\)

\(Y_{it} = \beta_0 + \beta_1 X_{it} + \beta_2Z_{i} + u_{it}, i =1,\dots,n, T = 1,\dots,T\)

We can rewrite this in two useful ways: 1. “\(n-1\) binary regressor” regression model 2. “Fixed Effects” regression model

We first rewrite this in “fixed effects” form. Suppose we have \(n = 3\) states: California, Texas, Massachusetts.

\(Y_{it} = \beta_0 + \beta_1 X_{it} + \beta_2Z_{i} + u_{it}, i =1,\dots,n, T = 1,\dots,T\)

Population regression for California (that is, \(i = CA\)): \(Y_{CA,t} = \beta_0 + \beta_1X_{CA,t} + \beta_2Z_{CA} + u_{CA,t}\\ = (\beta_0 + \beta_2Z_{CA}) + \beta_1X_{CA,t} + u_{CA,t}\) or \(Y_{CA,t} = \alpha + \beta_1X_{CA,t} + u_{CA,t}\)

• \(\alpha_{CA} = \beta_0 + \beta_1Z_{CA}\) doesn’t change over time • \(\alpha_{CA}\) is the intercept for CA, and \(\beta_1\) is the slope • The intercept is unique to CA, but the slope is the same in all the states: parallel lines.

\(Y_{it} = \beta_0 + \beta_1 X_{it} + \beta_2Z_{i} + u_{it}, i =1,\dots,n, T = 1,\dots,T\)

Population regression for Texax (that is, \(i = TX\)): \(Y_{TX,t} = \beta_0 + \beta_1X_{TX,t} + \beta_2Z_{TX} + u_{TX,t}\\ = (\beta_0 + \beta_2Z_{TX}) + \beta_1X_{TX,t} + u_{TX,t}\) or \(Y_{TX,t} = \alpha + \beta_1X_{TX,t} + u_{TX,t}\)

Collecting the like terms

\(Y_{CA,t} = \alpha + \beta_1X_{CA,t} + u_{CA,t}\)

\(Y_{TX,t} = \alpha + \beta_1X_{TX,t} + u_{TX,t}\)

\(Y_{MA,t} = \alpha + \beta_1X_{MA,t} + u_{MA,t}\)

or \(Y_{it} = \alpha_{i} + \beta_1 X_{it} + u_{it}, i =CA,TX,MA, T = 1,\dots,T\)

Regression equation for three states

In binary regressor form: \(Y_{it} = \beta_0 + \gamma CADCAi + \gamma TXDTXi + \beta_1X_{it} + u_{it}\) • \(DCA_{i} = 1\) if state is \(CA, = 0\) otherwise • \(DTX_{t} = 1\) if state is \(TX, = 0\) otherwise • leave out \(DMA_{i}\) (why?)

The Fixed Effects Regression Model

The fixed effect model is \(\begin{align} Y_{it} = \beta_1 X_{1,it} + \cdots + \beta_k X_{k,it} + \alpha_i + u_{it} \tag{10.3} \end{align}\) with \(i=1,\dots,n\) and \(t=1,\dots,T\) . The \(\alpha_i\) are entity-specific intercepts that capture heterogeneities across entities. An equivalent representation of this model is given by \(\begin{align} Y_{it} = \beta_0 + \beta_1 X_{1,it} + \cdots + \beta_k X_{k,it} + \gamma_2 D2_i + \gamma_3 D3_i + \cdots + \gamma_n Dn_i + u_{it} \tag{10.4} \end{align}\)
where the \(D2_i,D3_i,\dots,Dn_i\) are dummy variables.

Summary: Two ways to write the fixed effects model “n-1 binary regressor” form

\(Y_{it} = \beta_0 + \beta_1 X_{1,it} + \gamma_2 D2_i + \gamma_3 D3_i + \cdots + \gamma_n Dn_i + u_{it}\)

where \(D2i =1\) if \(i=2\) \(=0\) otherwise , etc.

“Fixed effects” form: \(Y_{it} = \beta_1X_{it} + \alpha_i + u_{it}\)

• \(\alpha_i\) is called a “state fixed effect” or “state effect” – it is the constant (fixed) effect of being in state \(i\).

Fixed Effects Regression: Estimation

Three estimation methods: 1. “n-1 binary regressors” OLS regression 2. “Entity-demeaned” OLS regression 3. “Changes” specification, without an intercept (only works for T = 2)

• These three methods produce identical estimates of the regression coefficients, and identical standard errors. • We already did the “changes” specification (1988 minus 1982) – but this only works for T = 2 years • Methods #1 and #2 work for general T • Method #1 is only practical when n isn’t too big

1. “n-1 binary regressors” OLS regression

\(Y_{it} = \beta_0 + \beta_1 X_{1,it} + \gamma_2 D2_i + \gamma_3 D3_i + \cdots + \gamma_n Dn_i + u_{it}\)

where \(D2i =1\) if \(i=2\) \(=0\) otherwise , - First create the binary variables D2i,…,Dni - Then estimate (1) by OLS - Inference (hypothesis tests, confidence intervals) is as usual (using heteroskedasticity-robust standard errors) - This is impractical when n is very large (for example if n = 1000 workers)

2. “Entity-demeaned” OLS regression

\[\begin{align*} \frac{1}{n} \sum_{i=1}^n Y_{it} =& \, \beta_1 \frac{1}{n} \sum_{i=1}^n X_{it} + \frac{1}{n} \sum_{i=1}^n a_i + \frac{1}{n} \sum_{i=1}^n u_{it} \\ \overline{Y} =& \, \beta_1 \overline{X}_i + \alpha_i + \overline{u}_i. \end{align*}\] Subtracting from 10.1 yields $$\[\begin{align} \begin{split} Y_{it} - \overline{Y}_i =& \, \beta_1(X_{it}-\overline{X}_i) + (u_{it} - \overline{u}_i) \\ \overset{\sim}{Y}_{it} =& \, \beta_1 \overset{\sim}{X}_{it} + \overset{\sim}{u}_{it}. \end{split} \tag{10.5} \end{align}\]$$

In this model, the OLS estimate of the parameter of interest \(\beta_1\) is equal to the estimate obtained using (10.2) — without the need to estimate \(n-1\) dummies and an intercept.

Application to traffic deaths

Panel Data for two years

Code 
# compute the differences 
diff_fatal_rate <- Fatalities1988$fatal_rate - Fatalities1982$fatal_rate
diff_beertax <- Fatalities1988$beertax - Fatalities1982$beertax

# estimate a regression using differenced data
fatal_diff_mod <- lm(diff_fatal_rate ~ diff_beertax)

coeftest(fatal_diff_mod, vcov = vcovHC, type = "HC1")

t test of coefficients:

              Estimate Std. Error t value Pr(>|t|)   
(Intercept)  -0.072037   0.065355 -1.1022 0.276091   
diff_beertax -1.040973   0.355006 -2.9323 0.005229 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Code 
df2<-cbind(diff_fatal_rate,diff_beertax)

df2<-as.data.frame(df2)
## Plot
p2<-ggplot(df2)+aes(x=diff_fatal_rate,y=diff_beertax)+geom_point()+
  geom_smooth(method = "lm",se=FALSE)
p2+labs(x = "Change in beer tax (in 1988 dollars)",
        y = "Change in fatality rate (fatalities per 10000)")+ggtitle("Changes in Traffic Fatality Rates and Beer Taxes in 1982-1988")
`geom_smooth()` using formula 'y ~ x'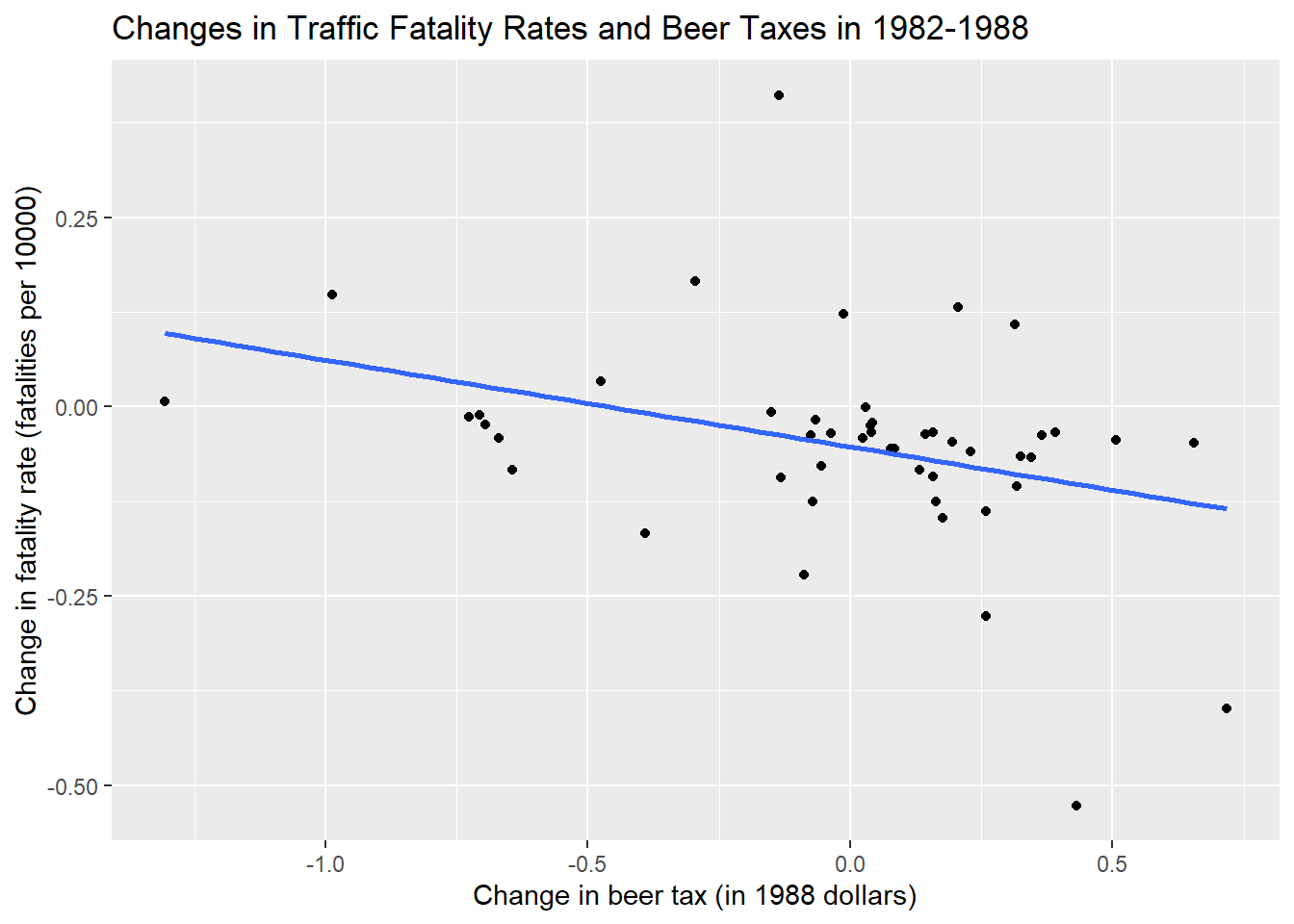

compute mean fatality rate over all states for all time periods

Code 
df %>% group_by(year) %>% 
  summarise(mean=mean(fatal_rate))
# A tibble: 7 × 2
  year   mean
  <fct> <dbl>
1 1982   2.09
2 1983   2.01
3 1984   2.02
4 1985   1.97
5 1986   2.07
6 1987   2.06
7 1988   2.07
Code 
mean(df$fatal_rate)
[1] 2.040444
Code 
df %>% select(fatal_rate) %>% 
  summarise(mean=mean(fatal_rate))
      mean
1 2.040444

\(\begin{align} FatalityRate_{it} = \beta_1 BeerTax_{it} + StateFixedEffects\\ + u_{it}, \tag{10.6} \end{align}\)

Code 
fatal_fe_lm_mod <- lm(fatal_rate ~ beertax + state - 1, data = df)
fatal_fe_lm_mod

Call:
lm(formula = fatal_rate ~ beertax + state - 1, data = df)

Coefficients:
beertax  stateal  stateaz  statear  stateca  stateco  statect  statede  
-0.6559   3.4776   2.9099   2.8227   1.9682   1.9933   1.6154   2.1700  
statefl  statega  stateid  stateil  statein  stateia  stateks  stateky  
 3.2095   4.0022   2.8086   1.5160   2.0161   1.9337   2.2544   2.2601  
statela  stateme  statemd  statema  statemi  statemn  statems  statemo  
 2.6305   2.3697   1.7712   1.3679   1.9931   1.5804   3.4486   2.1814  
statemt  statene  statenv  statenh  statenj  statenm  stateny  statenc  
 3.1172   1.9555   2.8769   2.2232   1.3719   3.9040   1.2910   3.1872  
statend  stateoh  stateok  stateor  statepa  stateri  statesc  statesd  
 1.8542   1.8032   2.9326   2.3096   1.7102   1.2126   4.0348   2.4739  
statetn  statetx  stateut  statevt  stateva  statewa  statewv  statewi  
 2.6020   2.5602   2.3137   2.5116   2.1874   1.8181   2.5809   1.7184  
statewy  
 3.2491

Demeaned Regressioin

\(\overset{\sim}{FatalityRate} = \beta_1 \overset{\sim}{BeerTax}_{it} + u_{it}.\)

Code 
# obtain demeaned data
Fatalities_demeaned <- with(df,
            data.frame(fatal_rate = fatal_rate - ave(fatal_rate, state),
            beertax = beertax - ave(beertax, state)))

# estimate the regression
summary(lm(fatal_rate ~ beertax - 1, data = Fatalities_demeaned))

Call:
lm(formula = fatal_rate ~ beertax - 1, data = Fatalities_demeaned)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.58696 -0.08284 -0.00127  0.07955  0.89780 

Coefficients:
        Estimate Std. Error t value Pr(>|t|)    
beertax  -0.6559     0.1739  -3.772 0.000191 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1757 on 335 degrees of freedom
Multiple R-squared:  0.04074,   Adjusted R-squared:  0.03788 
F-statistic: 14.23 on 1 and 335 DF,  p-value: 0.0001913

Use plm

Alternatively use plm package

Code 
library(plm)

Attaching package: 'plm'
The following objects are masked from 'package:dplyr':

    between, lag, lead
Code 
# estimate the fixed effects regression with plm()
fatal_fe_mod <- plm(fatal_rate ~ beertax, 
                    data = df,
                    index = c("state", "year"), 
                    model = "within")

# print summary using robust standard errors
coeftest(fatal_fe_mod, vcov. = vcovHC, type = "HC1")

t test of coefficients:

        Estimate Std. Error t value Pr(>|t|)  
beertax -0.65587    0.28880  -2.271  0.02388 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

\(\begin{align} \widehat{FatalityRate} = -\underset{(0.29)}{0.66} \times BeerTax + \\ StateFixedEffects. \tag{10.7} \end{align}\)

The coefficient on $BeerTax $ is negative and significant. The interpretation is that the estimated reduction in traffic fatalities due to an increase in the real beer tax by \(1\$\) is \(0.66\) per \(10,000\) people, which is still pretty high.

Regression with Time Fixed Effect

\(Y_{it} = \beta_0 + \beta_1 X_{it} + \delta_2 B2_t + \cdots\\ + \delta_T BT_t + u_{it},\) where \(T-1\) are binary variables (\(B_1\) is ommited) The entity time fixed effect is \(Y_{it} = \beta_0 + \beta_1 X_{it} + \gamma_2 D2_i + \cdots \\ + \gamma_n DT_i + \delta_2 B2_t + \cdots + \delta_T BT_t + u_{it} .\)

\(FatalityRate_{it} = \beta_1 BeerTax_{it} + StateEffects + \\TimeFixedEffects + u_{it}\)

Code 
# estimate a combined time and entity fixed effects regression model

# via lm()
fatal_tefe_lm_mod <- lm(fatal_rate ~ beertax + state + year - 1, data = df)
fatal_tefe_lm_mod

Call:
lm(formula = fatal_rate ~ beertax + state + year - 1, data = df)

Coefficients:
 beertax   stateal   stateaz   statear   stateca   stateco   statect   statede  
-0.63998   3.51137   2.96451   2.87284   2.02618   2.04984   1.67125   2.22711  
 statefl   statega   stateid   stateil   statein   stateia   stateks   stateky  
 3.25132   4.02300   2.86242   1.57287   2.07123   1.98709   2.30707   2.31659  
 statela   stateme   statemd   statema   statemi   statemn   statems   statemo  
 2.67772   2.41713   1.82731   1.42335   2.04488   1.63488   3.49146   2.23598  
 statemt   statene   statenv   statenh   statenj   statenm   stateny   statenc  
 3.17160   2.00846   2.93322   2.27245   1.43016   3.95748   1.34849   3.22630  
 statend   stateoh   stateok   stateor   statepa   stateri   statesc   statesd  
 1.90762   1.85664   2.97776   2.36597   1.76563   1.26964   4.06496   2.52317  
 statetn   statetx   stateut   statevt   stateva   statewa   statewv   statewi  
 2.65670   2.61282   2.36165   2.56100   2.23618   1.87424   2.63364   1.77545  
 statewy  year1983  year1984  year1985  year1986  year1987  year1988  
 3.30791  -0.07990  -0.07242  -0.12398  -0.03786  -0.05090  -0.05180

Via plm

Code 
# via plm()
fatal_tefe_mod <- plm(fatal_rate ~ beertax, 
                      data = df,
                      index = c("state", "year"), 
                      model = "within", 
                      effect = "twoways")

coeftest(fatal_tefe_mod, vcov = vcovHC, type = "HC1")

t test of coefficients:

        Estimate Std. Error t value Pr(>|t|)  
beertax -0.63998    0.35015 -1.8277  0.06865 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

state and year are the class factors:

Code 
# check the class of 'state' and 'year'
class(Fatalities$state)
[1] "factor"
Code 
#> [1] "factor"
class(Fatalities$year)
[1] "factor"
Code 
#> [1] "factor"

\(\begin{align} \widehat{FatalityRate} = -\underset{(0.35)}{0.64} \times BeerTax + StateEffects + TimeFixedEffects. \tag{10.8} \end{align}\)

The Fixed Effects Regression Assumptions

In the fixed effects model \(Y_{it} = \beta_1 X_{it} + \alpha_i + u_{it} \ \ , \ \ i=1,\dots,n, \ t=1,\dots,T,\) we assume the following: 1. The error term \(u_{it}\) has conditional mean zero, that is, \(E(u_{it}|X_{i1}, X_{i2},\dots, X_{iT})\). 2. \((X_{i1}, X_{i2}, \dots, X_{i3}, u_{i1}, \dots, u_{iT})\) are i.i.d draw from their distributions. 3. Large outliers are unlikely, i.e., \((u_{it},x_{it})\) have nonzero finite fourth moments. 4. There is no perfect multicollinearity. When there are multiple regressors, \(x_{it}\) is replaced with \(X_{1,it}, X_{2,it}, \dots, X_{k,it}\).

discretize the minimum legal drinking age

Code 
df$drinkagec <- cut(df$drinkage,
                            breaks = 18:22, 
                            include.lowest = TRUE, 
                            right = FALSE)

# set minimum drinking age [21, 22] to be the baseline level
df$drinkagec <- relevel(df$drinkagec, "[21,22]")

# mandadory jail or community service?
df$punish <- with(df, factor(jail == "yes" | service == "yes", 
                                             labels = c("no", "yes")))

estimate all seven models

Code 
Fatalities_1982_1988 <- df[with(df, year == 1982 | year == 1988),]
models<-list(fatalities_mod1 <- lm(fatal_rate ~ beertax, data = df),

fatalities_mod2 <- plm(fatal_rate ~ beertax + state, data = df),

fatalities_mod3 <- plm(fatal_rate ~ beertax + state + year,
                       index = c("state","year"),
                       model = "within",
                       effect = "twoways", 
                       data = df),

fatalities_mod4 <- plm(fatal_rate ~ beertax + state + year + drinkagec 
                       + punish + miles + unemp + log(income), 
                       index = c("state", "year"),
                       model = "within",
                       effect = "twoways",
                       data = df),

fatalities_mod5 <- plm(fatal_rate ~ beertax + state + year + drinkagec 
                       + punish + miles,
                       index = c("state", "year"),
                       model = "within",
                       effect = "twoways",
                       data = df),

fatalities_mod6 <- plm(fatal_rate ~ beertax + year + drinkage 
                       + punish + miles + unemp + log(income), 
                       index = c("state", "year"),
                       model = "within",
                       effect = "twoways",
                       data = df),
## the set of observations on all variables for 1982 and 1988
fatalities_mod7 <- plm(fatal_rate ~ beertax + state + year + drinkagec 
                       + punish + miles + unemp + log(income), 
                       index = c("state", "year"),
                       model = "within",
                       effect = "twoways",
                       data = Fatalities_1982_1988))



##We again use stargazer() (Hlavac, 2018) to generate a comprehensive tabular presentation of the results.

library(stargazer)

Please cite as: 
 Hlavac, Marek (2022). stargazer: Well-Formatted Regression and Summary Statistics Tables.
 R package version 5.2.3. https://CRAN.R-project.org/package=stargazer
Code 
library(sjPlot)
library(sjmisc)
Learn more about sjmisc with 'browseVignettes("sjmisc")'.

Attaching package: 'sjmisc'
The following object is masked from 'package:purrr':

    is_empty
The following object is masked from 'package:tidyr':

    replace_na
The following object is masked from 'package:tibble':

    add_case
Code 
library(sjlabelled)

Attaching package: 'sjlabelled'
The following object is masked from 'package:forcats':

    as_factor
The following object is masked from 'package:dplyr':

    as_label
The following object is masked from 'package:ggplot2':

    as_label
Code 
library(modelsummary)
modelsummary(models,fmt=3,vcov = "robust",estimate = "{estimate}{stars}",
             gof_omit = ".*",output = "gt")
Model 1 Model 2 Model 3 Model 4 Model 5 Model 6 Model 7
(Intercept) 1.853***
(0.047)
beertax 0.365*** -0.656* -0.640+ -0.445 -0.690+ -0.456 -0.926*
(0.054) (0.298) (0.366) (0.318) (0.370) (0.327) (0.382)
drinkagec[18,19) 0.028 -0.010 0.037
(0.074) (0.084) (0.112)
drinkagec[19,20) -0.018 -0.076 -0.065
(0.050) (0.067) (0.099)
drinkagec[20,21) 0.032 -0.100+ -0.113
(0.053) (0.057) (0.131)
punishyes 0.038 0.085 0.039 0.089
(0.111) (0.119) (0.110) (0.179)
miles 0.000 0.000 0.000 0.000*
(0.000) (0.000) (0.000) (0.000)
unemp -0.063*** -0.063*** -0.091***
(0.013) (0.013) (0.022)
log(income) 1.816** 1.786** 0.996
(0.646) (0.650) (0.715)
drinkage -0.002
(0.022)

Wage data Woolridge book

Code 
library(tidyverse)
library(wooldridge)
library(broom)
library(magrittr)

Attaching package: 'magrittr'
The following object is masked from 'package:purrr':

    set_names
The following object is masked from 'package:tidyr':

    extract
Code 
library(clubSandwich)
Registered S3 method overwritten by 'clubSandwich':
  method    from    
  bread.mlm sandwich
Code 
library(modelsummary)
library(estimatr)
library(plm)   # You may need to install this package

Load the data

Load the data Our data set will be a panel of wages for 545 men. Load the data from the wooldridge package, format year to be a factor, and rename the variable nr to something more descriptive (id):

Code 
df <- as_tibble(wagepan)
df %<>% mutate(year=as.factor(year))
df %<>% rename(id = nr)

Summary Statistics with Panel Data

Code 
df.within <- df %>% select(id,year,educ,married,union,rur) %>% 
             group_by(id) %>% 
             summarize(
                 mean.edu = mean(educ),
                 var.edu  = var(educ),
                mean.marr = mean(married),
                 var.marr = var(married),
               mean.union = mean(union),
                var.union = var(union),
               mean.rural = mean(rur),
                var.rural = var(rur)
             )
df.within %>% datasummary_skim()
Unique (#) Missing (%) Mean SD Min Median Max
id 545 0 5262.1 3499.0 13.0 4569.0 12548.0
mean.edu 13 0 11.8 1.7 3.0 12.0 16.0
var.edu 1 0 0.0 0.0 0.0 0.0 0.0
mean.marr 9 0 0.4 0.4 0.0 0.4 1.0
var.marr 5 0 0.1 0.1 0.0 0.1 0.3
mean.union 9 0 0.2 0.3 0.0 0.1 1.0
var.union 5 0 0.1 0.1 0.0 0.0 0.3
mean.rural 9 0 0.2 0.4 0.0 0.0 1.0
var.rural 5 0 0.0 0.1 0.0 0.0 0.3

Is there any within-person variance in the educ variable? What about married, union, and rural?

What does it mean for the married, union, or rural variables to have a positive within-person variance?

Why is it important to know if a variable has positive within-person variance?

Pooled OLS, Random Effects, and Fixed Effects Models

\(\begin{align*} \log(wage_{it}) & = \beta_0 + \beta_1 educ_{i} + \beta_2 black_{i} + \beta_3 hisp_{i} + \beta_4 exper_{it} + \beta_5 exper_{it}^2 + \beta_6 married_{it} + \\ &\phantom{=\,\,}\beta_7 union_{it} + \beta_8 rur_{it} + \sum_t \beta_{9,t}year_{it} + a_i + u_{it} \end{align*}\) The pooled ols by lm_robust

Code 
est.pols <- lm_robust(lwage ~ educ + black + hisp + exper + I(exper^2) + married + union + rur + year,
                data = df, clusters=id)

Interpret the coefficient on β7 in the pooled OLS model

Random effects

Code 
est.re <- plm(lwage ~ educ + black + hisp + exper + I(exper^2) + married + union + rur + year, 
              data = df, index = c("id","year"), model = "random")

What is the estimate of \(θ\) in the RE model? (Hint: check est.re$ercomp$theta) What does this tell you about what you expect the random effects estimates to be relative to the fixed effects estimates?

Fixed effects

FE also come from the lm_robust() function:

Code 
est.fe <- lm_robust(lwage ~ I(exper^2) + married + union + rur + year, 
              data = df, fixed_effects = ~id)

Explain why we cannot estimate coefficients on \(educ\), \(black\), \(hisp\), or \(exper\) in the fixed effects model. (Note: the reason for not being able to estimate exper is more nuanced)

##Clustered standard errors The most appropriate standard errors account for within-person serial correlation and are robust to heteroskedasticity.

Code 
clust.re <- coef_test(est.re, vcov = "CR1", cluster = "individual")
clust.re.SE <- clust.re$SE
names(clust.re.SE) <- names(est.re$coefficients)

Model summary

Code 
modelsummary(list("POLS"=est.pols,"RE"=est.re,"FE"=est.fe),
             statistic_override=list(sqrt(diag(est.pols$vcov)),clust.re.SE,sqrt(diag(est.fe$vcov))),
             output="markdown")
POLS RE FE
(Intercept) 0.165 0.036
(0.163) (0.161)
educ 0.087 0.091
(0.011) (0.011)
black -0.149 -0.141
(0.051) (0.051)
hisp -0.016 0.016
(0.040) (0.040)
exper 0.069 0.106
(0.019) (0.016)
I(exper^2) -0.002 -0.005 -0.005
(0.001) (0.001) (0.001)
married 0.126 0.065 0.047
(0.026) (0.019) (0.018)
union 0.182 0.107 0.079
(0.028) (0.021) (0.019)
rur -0.138 -0.023 0.049
(0.035) (0.031) (0.031)
year1981 0.053 0.040 0.152
(0.028) (0.028) (0.027)
year1982 0.055 0.030 0.254
(0.037) (0.035) (0.028)
year1983 0.049 0.019 0.357
(0.046) (0.044) (0.032)
year1984 0.074 0.041 0.494
(0.057) (0.055) (0.040)
year1985 0.090 0.056 0.622
(0.066) (0.064) (0.048)
year1986 0.120 0.089 0.771
(0.076) (0.075) (0.059)
year1987 0.151 0.132 0.931
(0.085) (0.085) (0.070)
Num.Obs. 4360 4360 4360
R2 0.199 0.181 0.621
R2 Adj. 0.178
AIC 5944.3 3304.4 2670.4
BIC 6052.8 3412.9 2746.9
RMSE 0.48 0.35 0.33